Min-Max et Alpha-Beta sont des algorithmes classiques des stratégies de
jeux. Pour être efficace, l'utilisation de ces algorithmes devra être
basée sur une analyse correcte du jeu.
Algorithme
Min-Max
1
- Définition Théorique
- Principe
¤ Définition d'un arbre de choix
Ces Algorithmes se basent sur des arbres de choix qui énumèrent le plus
de coups possible. Leur représentation est la suivante :
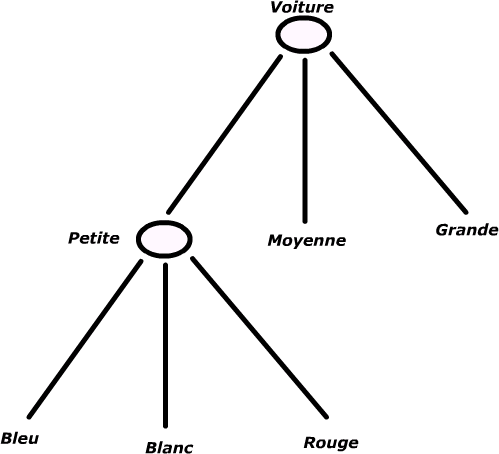
Dans le cas de
Min-Max et Alpha-Beta, le choix est représenté par un nœud et une note
(évaluation de la position), de ce nœud découle des branches qui se dirigent
vers d'autres nœuds qui sont en fait les autres choix possibles à partir
du choix effectué représenté par le nœud père.
Tout à fait à part on peut étudier voir le fonctionnement de l'arbre de
choix suivant.
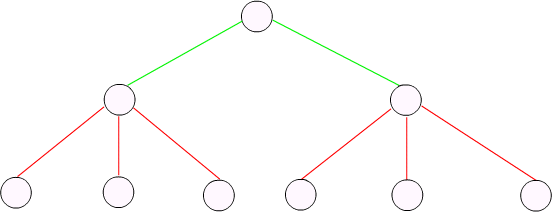
Voiture : Couleur[bleu,blanc,rouge];
Taille[Grande,Moyenne,Petite];
¤ Description des 3 paramètres
Pour un algorithme
de type Min-Max, il y a trois paramètres qui déterminent la qualité de
recherche du meilleur coup :
- Profondeur de Recherche. (L'Arbre, nombre de coups calculés)
-
La fonction d'évaluation stratégique. (Le Score, évaluer la position d'un
joueur)
- La vitesse à laquelle nous pouvons analyser le jeu. (Le délai d'attente
de réponse)
Ces trois critères sont fortement liés. Par exemple, si nous pouvions
facilement générer l'arbre complet des 60 coups du jeu grâce au critère
de temps, nous n'aurions besoin que d'une fonction d'évaluation non stratégique,
retournant 2 états (gagné ou perdu [1, -1]) - ce qui sera le cas du morpion
- ainsi que d'un algorithme de génération d'arbre le plus simple possible.
L'ordinateur gagnerait à tous les coups, ou ferait au minimum égalité.
Si au contraire nous ne pouvons pas générer l'arbre complet, c'est très
souvent le cas, nous aurons tout intérêt à utiliser une fonction d'évaluation
capable de dire si tel ou tel joueur est plutôt bien ou mal positionner
pour gagner. Mais, ici un problème se pose, mieux vaut-il utiliser une
fonction d'évaluation poussée qui prendra plus de temps, et descendre
moins loin en profondeur dans l'arbre, ou faut-il négliger un peu plus
la fonction d'évaluation et descendre plus loin dans les arbres générés
?
Il n'existe pas de formule simple pour trouver les meilleurs compromis.
Le mieux est alors d'effectuer une série d'essais jusqu'à trouver une
solution qui convienne au programme.
2 -
Exemple d'application
Il est difficile de s'étaler sur du théorique, c'est pour cela que nous
passons assez rapidement à la partie pratique. Le choix des jeux est le
suivant : L'Othello et le Morpion. L'Othello sert à montrer la complexité
de l'arbre, ainsi que l'importance de la dépendance des 3 paramètres.
Surtout pour la fonction d'évaluation. Par contre le Morpion, sert à vraiment
montrer le code dans la pratique, le plus simplement possible, car il
n'est pas compliqué et permet d'évaluer tous les cas possibles sans trop
de problèmes.
- Jeu complexe : Othello
¤ Pourquoi l'Othello ?
Il aurait été possible de prendre, comme exemple de jeu complexe, un autre
jeu tel que les échecs, ce jeu est souvent pris en exemple, donc très
documenté, mais les arbres sont complexes à élaborer. Une bonne analyse
d'une partie demande déjà beaucoup d'expérience dans le domaine du jeu.
Nous avons donc choisit l'Othello, d'une part parce qu'il est bien documenté
et c'est un jeu où tout peut se renverser très vite, ce qui demande une
bonne évaluation de la position de l'ordinateur.
¤ Description du principe du jeu
Le jeu de l'Othello est aussi connu sous le nom de Reversi. Le principe
du jeu est le suivant :
la surface de jeu se présente ainsi :
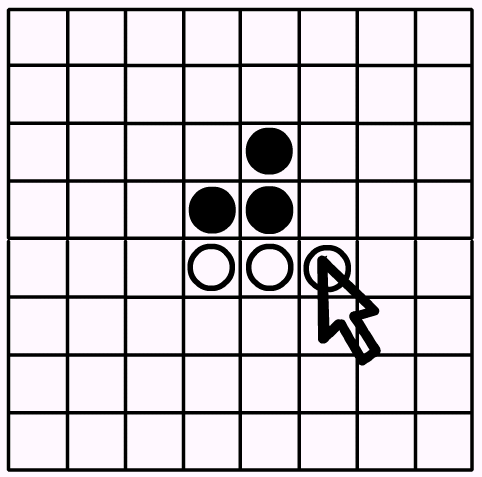
La surface de
jeu : C'est un damier de 8 cases sur 8 cases, avec 64 pions qui a
une face blanche et une face noire.
But du jeu : Avoir le plus de pions de sa couleur à la fin de la
partie.
Le jeu : Chaque joueur à son tour doit jouer sur une case du plateau.
Il doit encadrer au moins 1 pion de la couleur adverse. Les pions encadrés
se retournent pour devenir de la couleur du joueur. Un joueur passe s'il
ne peut pas encadrer de pions adverses. Si les 2 joueurs passent, la partie
se termine et celui qui a le plus de pions gagne. Si les 2 joueurs ont
le même nombre de pions en fin de partie, celle-ci est nulle.
¤ Description du découpage de la partie Algorithmique
1) Représentation Informatique
Nous allons faire une représentation des objets réels sous
forme d'objet en programmation, tout de même, il faut préciser que nous
n'entrons pas dans les détails du format de ces donnés et de leur représentation
en mémoire.
On créé donc les objets suivants :
Damier[1..8][1..8] : Surface de jeu qui contient de objets pions.
C'est un Type d'objet.
PionNoir, PionBlanc : Type de Pion qui remplit le damier.
Coup : Contient les coordonnés x, y d'un pion entre 1 et 8, ainsi
que la couleur du joueur.
Score : Contient le résultat de l'évaluation du jeu.
Possibilités[1..33] : Contient le nombre de coups possibles.
On a donc une variable globale que l'on nomme "DamierDeJeu" qui est le
damier affiché à l'écran, c'est le jeu en cours. Maintenant que nous avons
définit nos Types il faut définir les différentes fonctions que nous allons
utiliser pour le jeu.
2)
Le Découpage du jeu en fonctions
1) La fonction de recherche de coups possibles :
On appelle cette fonction : Evalue_Les_Coups_Possibles();
Paramètres de cette fonction :
LeDamier : LeDamier de jeu à évaluer (pas forcément le damier de
jeu courant).
Couleur : Couleur du joueur dont on doit donner le nombre de coups
possibles.
Variables retournés par la fonction :
Possible[1..32] : Tableau d'objets Coup qui représente les
Coups Possibles.
On sait par expérience qu'il est impossible de pouvoir jouer plus de 32
coups.
NombreDeCoups : Valeur du nombre de coups.
Description :
Cette fonction est simple à décrire : on lui donne en paramètres le
damier à étudier, et la couleur du joueur dont on doit évaluer le nombre
de coups possibles. Cette fonction retourne un tableau d'une capacité
de 32 Coups qui sont tous le coups possible réalisables par le joueur
de la couleur spécifiée en paramètre d'entré. Il est aussi possible d'admettre
que "Possible[0]" contient le nombre de coups jouables, c'est plus facile
à gérer.
L'ajustement de la taille du tableau possible[33] : Il existe un nombre
N qui est le nombre maximum de coups jouables pour un joueur donné, pour
tout damier possible. Nous sommes sûrs que N < 60 (car à la base, il y
a 64-4 places libres). Le calcul de N est très complexe à déterminer.
Par l'expérience nous n'avons jamais atteint plus de 20 coups jouables
lors d'une partie. On pose alors un N = 32, en supposant que le nombre
de coups effectivement possibles ne dépasse jamais ce nombre. De plus,
nous n'avons pas trouvé de placement arbitraire de pions tel qu'il y a
autant de coups jouables. Même si nous y arrivons, il est très probable
que la configuration trouvée ne soit pas accessible par un jeu ayant débuté
de manière conventionnelle.
Dans notre représentation sous forme d'arbre, le nombre de coups possibles
correspond au nombre de branches qui sont issues du damier père.
2) La fonction qui applique un coup sur le damier
:
On appelle cette fonction : Appliquer_Mouvement();
Paramètres de cette fonction :
LeDamier : Le Damier sur lequel de coup est appliqué. le damier
est retourné modifié. Pas forcément de damier déclaré globalement.
Coup : Coup a appliquer sur le damier.
Description :
D'un point de vue algorithmique, cette fonction est proche de la
fonction 'coup_possible'. Elle applique le coup qu'on lui donne, en retournant
les pions adverses sur le damier (dont on a passé l'adresse en paramètre).
Elle est essentiellement utilisée par - pour l'étude du jeu. L'algo de
cette procédure est tel qu'il n'y a pas de distinction entre un coup légal
ou non. Si le coup n'est pas valide, il n'y aura simplement et naturellement
aucun pion retourné, et aucun pion déposé. Cette fonction permet d'applique
un coup et d'en retourner le nouveau damier.
3) L'évaluation du damier :
!! C'est la fonction qui demande à la fois le plus d'astuce et le plus de soins de la part du programmeur. !!
On appelle cette fonction : Evaluation_Du_Damier();
Paramètres de cette fonction :
LeDamier : Le damier dont la position doit être évaluée.
Valeurs de Retour :
Score : Score attribué à la position du damier.
Description :
L'élaboration de cette dernière n'est pas évidente. Il n'existe pas
de solution précise, claire et nette pour évaluer un damier. Cette fonction
exige une bonne analyse et compréhension de la stratégie du jeu d'Othello
de la part du développeur.
Il s'agit en effet de donner une note globale à un damier statique, respectant
l'inégalité
[
- Max_note < NOTE < +Max_note ]
Max_Note :
une note positive déterminant une situation gagnée. (ie 20000)
Un damier dont la note se situe entre 1 et +Max_note est un damier où
le jeu est favorable aux Noirs (conventionnellement).
En revanche une note comprise entre -1 et -Max_note représente un jeu
défavorable aux pions Noirs, et donc favorable aux pions Blancs.
Nous sommes indécis pour une note nulle. Il vient immédiatement que si
un damier donne une note S, ce même damier avec tous les pions retournés
donnera la note -S.
Dans un premier temps, cette fonction n'était vouée qu'à différencier
le nombre de pions Noirs par rapport aux Blancs. Le principe était le
suivant : une case vide apporte 0 point, une case occupée par un pion
Noir apporte 1 point, une case occupée par un pion Blanc apporte -1 point
à la note globale du damier.
Améliorations réalisables pour une fonction d'évaluation stratégique
:
Bien sur la fonction devait aussi être capable de détecter une situation
totalement gagnée. Mais le critère du joueur qui dispose le plus de pions
n'est en fait pas significatif, même lorsque la fin du jeu est proche.
Le graphique ci-dessous tente de montrer les performances d'une telle
fonction par rapport à une fonction d'évaluation pouvant analyser un minimum
de stratégie, et par rapport à une fonction d'évaluation que nous aurions
souhaitée (idéale).
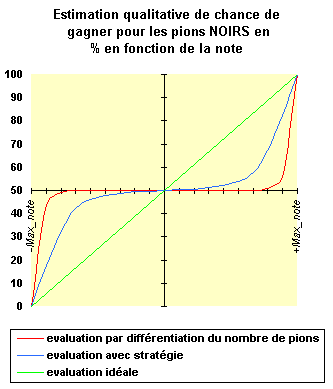
Le problème
est plus complexe : ces courbes dépendent du joueur humain. Si le
joueur humain utilise exactement la même stratégie que la fonction d'évaluation,
alors nous nous approcherons de très près du graphe dit 'idéal' !
Nous nous sommes finalement limités à faire une fonction d'évaluation
stratégique, qui tenait compte :
* de la mobilité de chaque joueur (combien Noir peut-il jouer de coups
différents pour un damier donné par rapport à Blanc). Par ce système relativement
rapide, le programme va tenter de bloquer son adversaire, ce qui aboutira
à la technique dite du bétonnage. De plus les pions posés par la machine
seront automatiquement assez stables.
* des coins en leur attribuant des points d'autant plus élevés que nous
sommes proches du début du jeu.
* du pourtour du damier, et attribue des points aux pions de bords, suivant
les coins, et suivant qu'un bord est plein ou non.
* Des cas des cases X (2,2 ;7,7 etc..) et C (1,2 ; 7,1 ...) qui ne seront
pas négligées. Elles donneront quant à elles des points négatifs si le
coin concerné n'est pas pris.
Ensuite reste le calibrage des proportions entre la mobilité, la stabilité
définitive des pions des bords, les coins et les cases X /C.
Plus d'une cinquantaine de jeux complets contre le logiciel d'Othello
THOR, une dizaine contre joueur humain ont été nécessaire pour aboutir
à un réglage satisfaisant de tous ces paramètres.
3)
Réalisation de l'arbre MinMax :
Description
Cet algorithme est essentiel, et on peut l'utiliser dans chaque jeu,
où il y a notion d'équilibre entre 2 adversaires.
Son principe est simple : il cherche le meilleur compromis parmi plusieurs
coups jouables, pour un joueur donné. Autrement dit, il va chercher en
profondeur trois par exemple, le meilleur coup du plus mauvais du meilleur.
('Mauvais' coup signifie meilleur coup pour les Blancs). on peut dire
Max-Min-Max Ainsi, quand la machine joue un coup, elle se garantit d'avoir
dans le Pème coups à venir (P = profondeur), au moins une note égale à
l'un des coups joués à la profondeur P.
L'exemple suivant qui développe un arbre - Min Max, traduit bien ce principe.
Nous sommes en profondeur 3 et chaque nœud représente un damier, et donc
un jeu différent.
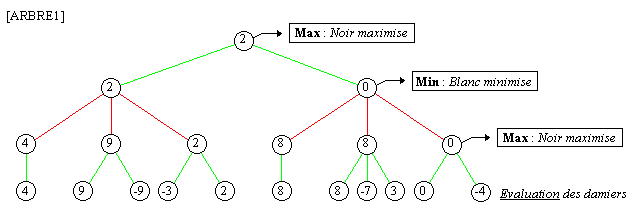
La note minimale
garantie pour le joueur Noir est 2, pour les 3 coups à venir.
Particularité de Min-Max appliqué au jeu d'Othello :
Contrairement aux échecs, quand une situation est bloquée pour un
joueur (pat) , le joueur pat rend la main à son adversaire. Ceci a pour
conséquence d'avoir dans l'arbre 2 transitions de même types entre 3 générations.
Nous aurons donc Max-Max ou Min-Min. Ce système est valable par générations
2 à 2. On peut donc avoir une succession de n fois la même transition.
Au premier appel de la fonction, on donne un damier à analyser, le niveau
de profondeur désiré, le joueur qui a la main et une variable "Coup".
On récupère une variable "coup". Les autres paramètres ne sont utiles
qu'à la récursivité de Min-Max.
On peut aussi souligner qu'il est plus simple de construire la procédure
Min-Max à partir d'un exemple d'arbre plutôt que d'essayer d'adapter des
algorithmes Min-Max crée par d'autre. C'est ce que l'on va voir avec le
morpion.
Définition de la fonction Min-Max :
On appelle la fonction : MiniMax();
Paramètres d'entrée :
LeDamier : Damier sur lequel on joue.
Profondeur : Profondeur de l'arbre de recherche.
Joueur : Joueur en cours (Blanc/Noir).
Variables retournées :
Coup : Coup à jouer.
Score : Score du coup.
Commentaires sur la programmation des fonctions
En moyenne, on peut compter 8 coups par damiers. En profondeur 10,
on dépasse déjà largement le milliard de nœuds. Néanmoins, nous ne devrions
jamais avoir de saturation de piles par l'empilement implicite de Min-Max
: il n'y a qu'un empilement d'une liste de coup et d'un damier chaque
fois que l'on descend d'un niveau dans l'arbre. Or, non seulement descendre
en profondeur 10, révèle d'un exploit de patience de la part de l'utilisateur
du jeu, mais en plus cela n'occupera pas plus de 2 ou 3 % des 64 Ko réservés
à la pile.
4) Programmation d'un othello en C : ( N'apparaît
pas à l'exposé )
Ici juste à titre d'indication pour approfondir la méthode. J'ai
mis ici le code en C que j'ai largement commenté, l'exemple de code est
issu du site web du projet LOthello réalisé par des étudiants (cf. liens).
Je n'ai pas eut le temps d'adapter cette procédure du C vers le Pascal,
j'ai préféré privilégier la simplicité et la clarté du code source d'un
morpion que j'ai codé en Pascal sans aucun exemple, ni code source (cf.
Plus loin).
Si on définit les prototypes de fonction de la manière suivante :
Le prototype : int coup_possibles (octet board[10][10] ,octet
possibles[33], octet couleur) ;
Le prototype : void apply_move (octet new_board[10][10],
octet* move);
Le prototype : int evaluation_damier (octet le_damier[10][10]);
Le prototype : void minimax (octet board[10][10], octet
depth, octet joueur, octet* move, int* score)
Min-Max en C :
{
int i, the_score; // Déclare les variables
octet new_board[10][10], liste[33], the_move; // - idem -
if ( !coup_possibles(board,liste,joueur) ) // S'il est impossible de jouer le coup ?
// -> Et au passage on récupère la liste des coups pour le joueur
if ( !coup_possibles(board, liste, joueur = -joueur+3) )
// Si on arrive à cette ligne, c'est que le joueur est bloqué.
{
// On va donc inverser le joueur (cas Max-Max ou Min-Min)
*score = evaluation_damier(board);
return; // On quitte la fonction
}
if (joueur == 1) // On évalue avec le joueur ordinateur
*score = -Max_note; // On inverse la note maximale et on l'attribut à score
else // Sinon...
*score = Max_note; // ...On attribut la note maximale
depth--; // On décrémente la profondeur
for (i = 1; i <= *liste; i++)// Maintenant on parcours toute la liste de coups possibles
{
memcpy(new_board, board, 100); // On duplique le tableau original
apply_move(new_board, liste+i);// ->Et en plus on applique le coup
if ( depth != 0 ) // S'il y a encore quelque chose à explorer ?
// ici on est à un noeud de l'arbre
minimax(new_board, depth, -joueur+3, &the_move, &the_score);
// On continue ainsi l'exploration de l'arbre MinMax, par la recursivité
else
// ici, on est aux feuilles de l'arbre.
the_score = evaluation_damier(new_board);
// On est au bout et on remonte tout l'arbre
if (joueur == 1) // Procédure Max en marche
{
if (the_score >= *score)
{
*score = the_score;
*move = liste[i];
}
}
else // Procédure Min en marche
{
if (the_score <= *score)
{
*score = the_score;
*move = liste[i];
}
}
} // -- Fin de la procedure MinMax en C --
¤ Pourquoi un arbre simple ?
Comme nous l'avons appris lors de l'étude de l'Othello, il vaut
mieux partir d'un arbre et arriver à du code source, c'est plus sûr que
faire l'inverse. Regardons comment marche une partie de Morpion, et voyons
comment nous visualisons l'évolution du jeu.
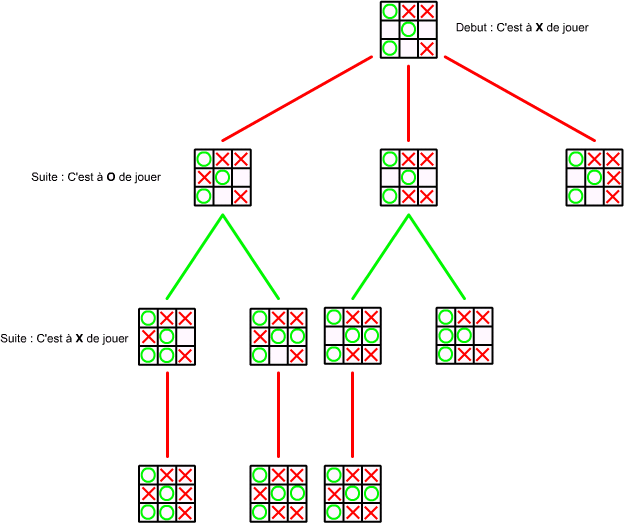
Voilà, sans le
savoir nous avons créé notre procédure MinMax, il suffit juste de la coder
en pascal. Le but de ce cours sur les algorithmes est de vous permettre
de coder un jeu avec une intelligence artificielle.
¤ Description du découpage algorithmique
Comme pour l'Othello, nous avons besoin de nombreuses fonction
qui nous permettent de programmer le jeu. Mais contrairement à l'exemple
de l'Othello, j'ai réalisé un code pascal que nous allons étudier ensemble,
ce qui est déjà très intéressant. Je tient tout de même à vous prévenir,
j'ai donné priorité à la lisibilité en laissant tomber les possibilités
d'optimisation.
1) Les objets et variables :
Au début du programme sont déclarés différents types et variables
globales, voilà l'explication des objets :
const VIDE
= 0; {case vide} CROIX = 1; {case occupée par un joueur croix} ROND =
2; {case occupée par un joueur rond } ici nous définissons les constantes
de valeurs possibles des case du tableau morpion. déclaration des types
: ici, nous avons la création du type morpion qui représente le niveau.
type morpion = array[1..3,1..3] of byte; { tableau de 3 par 3 qui représente
le morpion } definition d'un coup : coup = record { structure de coup
} x : byte; { position du coup } y : byte; coul : byte; { couleur du joueur
qui exécute le coup } end; définition d'une liste de coups possibles :
coupjeu = record { structure qui contient les coups possibles } ncoups
: byte; { nombre de coups jouables } coups : array[1..9] of coup; { les
différents coups jouables } end; définition de la variables globale :
var themorpion : morpion; { le morpion du jeu } il est certain que je
déclare comme variables globales d'autres variables, mais elles ne sont
utiles qu'à l'affichage donc elles n'ont aucun intérêt.
2) Les fonctions :
Il existe de nombreuses fonctions d'affichage et de débuggage,
mais je ne les présente pas ici. Nous allons nous intéresser à la programmation
des fonctions principales du morpion. Il s'agit des fonctions suivantes
: appliquer le coup, trouver les coups possibles, évaluation du jeu, et
Minmax.
a) Application du coup
{ Procedure qui applique le nombre de coups possibles }
Procedure applique_le_coup( var jeu:morpion; lecoup:coup);
begin
{ applique tout betement le coup }
jeu[lecoup.x,lecoup.y] := lecoup.coul;
end; {********* applique_le_coup ***********}
On donne à cette fonction un jeu de morpion et un coup, et il effectue
tout simplement le coup en remplissant la case du coup par la couleur
indiquée.
b) Fonction qui énumère les coups possibles
Cette fonction récupère une structure coupjeu qu'il doit remplir avec
les coups possibles sur un jeu de morpion donné, pour un joueur indiqué.
{ Fonction qui revoit le nombre de coups possibles }
function coup_possibles( var couppos:coupjeu; jeu:morpion; joueur:byte ):byte;
var i,j : byte;
begin
{ Remet à 0 le nombre de coups possibles }
couppos.ncoups := 0;
{ Parcours le tableau }
for i := 1 to 3 do
for j := 1 to 3 do
begin
{ Si la place est vide, noter comme un coup possible }
if ( jeu[i,j] = VIDE ) then
begin
{ incrémente le nombre de coups }
inc(couppos.ncoups);
{ ajoute le coup à la liste }
couppos.coups[couppos.ncoups].x := i;
couppos.coups[couppos.ncoups].y := j;
couppos.coups[couppos.ncoups].coul := joueur;
end;
end;
{ Retourne le nombre de coups possibles }
coup_possibles := couppos.ncoups;
end; {********* coup_possibles ***********}
Cette fonction est très simple, elle parcours le tableau de jeu et dès
qu'elle trouve une case vide elle enregistre la position de cette case
dans la structure couppos. De plus, cette fonction retourne directement
le nombre de coups possibles pour simplifier le code de Minmax.
c) le fonction d'évaluation
Pour un jeu où il est dur de parcourir tout l'arbre minmax, la fonction
d'évaluation doit être le plus soigné possible, c'est elle qui détermine
la valeur du coup joué.
La fonction prend comme paramètre d'entrée un jeu de morpion à évaluer,
et retourne une valeur entre -1 et 1 en entier, ce qui donne juste le
choix de -1, 0, 1. La valeur de retour -1 indique que le joueur ROND gagne
et la valeur 1 indique que la CROIX à gagné. Une valeur 0 indique une
position soit nulle, soit indéterminée (il reste des case vides).
{ Fonction qui évalue le jeu // pour le moment seulement gagné(1)-perdu(-1)}
function evaluation_du_jeu( var jeu:morpion ):integer;
var i,j : byte;
cx,cy : byte;
joueur: byte; { joueur evalué }
finit : boolean;
cool : boolean; { definit que le joueur est bien partit }
label gagne;
begin
{ definit comme + le score du joueur croix }
{ on commence par les croix ensuite on fait les ronds }
for joueur := CROIX to ROND do
begin
{ definit comme non finit }
finit := false;
cool := true;
{ parcours le tableau pour XXX (horizontal) }
for cy := 1 to 3 do
begin
{ initialise la recherche en x }
cx := 1;
cool := true;
repeat
{ verifie si le suivant est bon ->X }
cool := cool and (jeu[cx,cy] = joueur);
if (cx = 3) and cool then
finit := true;
inc(cx);
until (not cool) or (finit) or (cx=4);
{ quitte si c'est déjà finit pou les XXX (horizontal) }
if finit then
goto gagne;
end;
{ parcours le tableau pour X
X
X (Vertical) }
for cx := 1 to 3 do
begin
{ initialise la recherche en y }
cy := 1;
cool := true;
repeat
{ verifie si le suivant est bon |
v
X }
cool := cool and (jeu[cx,cy] = joueur);
if (cy = 3) and cool then
finit := true;
inc(cy);
until (not cool) or (finit) or (cy=4);
{ quitte si c'est déjà finit pou les X
X
X (Vertical) }
if finit then
goto gagne;
end;
{ parcours le tableau pour X
X
X (Obliques) }
begin
cx := 1;
cool := true;
repeat
{ verifie si le suivant est bon ->X }
cool := cool and (jeu[cx,cx] = joueur);
if (cx = 3) and cool then
finit := true;
inc(cx);
until (not cool) or (finit) or (cx=4);
{ quitte si c'est déjà finit pou les X
X
X (Obliques) }
if finit then
goto gagne;
end;
{ parcours le tableau pour X
X
X (Obliques) }
begin
cx := 1;
cool := true;
repeat
{ verifie si le suivant est bon ->X }
cool := cool and (jeu[cx,4-cx] = joueur);
if (cx = 3) and cool then
finit := true;
inc(cx);
until (not cool) or (finit) or (cx=4);
{ quitte si c'est déjà finit pou les X
X
X (Obliques) }
if finit then
goto gagne;
end;
end;
{ renvoi 0 pour une position non définie }
evaluation_du_jeu := 0;
{ label de gagné }
gagne :
{ verifie si ce n'est pas l'arrivé par défaut }
if finit then
if joueur = CROIX then
{ le joueur Croix etait évalué donc c'est 1 }
evaluation_du_jeu := 1
else if joueur = ROND then
{ ah, bon, le joueur rond était évalué donc c'est -1 }
evaluation_du_jeu := -1
end; {********** Evaluation du jeu *************}
Nous avons donc vérifié tous les cas de victoire possibles suivant les
positions des pions, cette fonction est assez simple malgré sa taille,
nous vérifions tous les alignements possibles, il existe sûrement un algorithme
moins conséquent, mais celui-ci semble clair.
Ah, vous avez sûrement remarqué la présence de goto et de label, c'est
vrai que c'est pas très propre comme programmation (personnellement je
n'utilise jamais cette méthode), mais bon, ca simplifie grandement la
clareté du code, un imbriquement de if...then...else embrouillait le code
plus qu'autre chose, encore désolé.
3) La procédure MinMax :
Nous voilà sur la procédure la plus complexe de tout le jeu, la
procédure Min-Max. Je pense que vous avez remarqué que j'avais précisé
pour l'exemple de l'Othello qu'il ne fallait par repiquer une procédure
minmax, mais plutôt repartir de l'arbre et reconstituer l'algorithme.
( Cette démonstration est visible lors de l'exposé ).
Ici nous allons nous contenter d'observer cette procédure récursive.
procedure minmax( jeu:morpion; depth:byte; joueur:byte;
{ valeurs retournées }
var lecoup:coup; var score:integer );
var
i, MM_score : integer;
MM_board : morpion;
couppos : coupjeu;
MM_move : coup;
begin
{ decrémente la profondeur de recherche }
dec( depth );
{ on verife si il y a encore des coups possibles }
if ( coup_possibles( couppos, jeu, joueur ) <> 0 ) then
begin
if joueur = CROIX then
score := -2
else
score := 2;
{ execute tous les coups possibles }
for i := 1 to couppos.ncoups do
begin
{ on recopie le jeu en mémoire }
move( jeu, MM_board, sizeof( morpion ) );
{ on applique le mouvement de la liste }
applique_le_coup( MM_board, couppos.coups[i] );
{ si il y a encore de la profondeur de recherche ;) }
{ et que c'est PAS une fin de partie (gagné ou perdu) }
if ( depth <> 0 ) and ( evaluation_du_jeu( MM_board ) = 0 ) then
{ appel minmax avec la reccursivité }
{ ici on est à un noeud de l'arbre }
minmax( MM_board, depth, inversejoueur(joueur), MM_move, MM_score )
else
{ ici, on est aux feuilles de l'arbre. }
begin
MM_score := evaluation_du_jeu( MM_board );
end;
display_coup_possibles( couppos , 60, 20 );
display_morpion( MM_board, 60, 15 );
if (joueur = CROIX) then
begin
if (score <= MM_score) then
begin
score := MM_score;
lecoup := couppos.coups[i];
end
end
else { if joueur = ROND then }
if (score >= MM_score) then
begin
score := MM_score;
lecoup := couppos.coups[i];
end;
end;
end;
end;
Cette procédure,
par sa récursivité construit un arbre de la profondeur donnée lors du
premier appel. Par exemple avec l'appel suivant vous pourrez retrouver
l'arbre suivant :
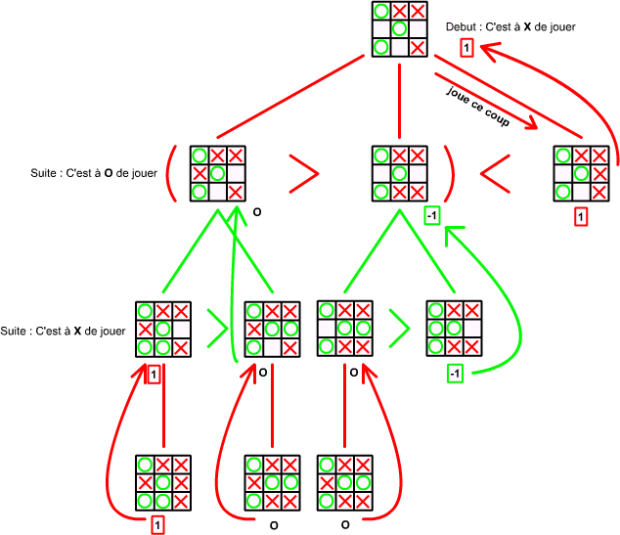
4)
Conclusion sur la création du jeu :
Avant de retourner à nos algorithmes, nous allons conclure sur
la création de l'IA d'un jeu. Avant tout, je pense que l'IA de votre jeu
sera bien plus complexe que celle d'un morpion, vous devez donc vous appliquer
sur les points suivants : La fonction d'évaluation : portez le plus grand
soin à cette fontion, plus elle est précise et efficace, moins vous avez
à explorer l'arbre de choix. La procédure MinMax : la procédure MinMax
est bien pratique mais peut-être un peu lente pour un arbre de choix assez
grand, il est donc obligatoire de l'optimiser, suivez bien, vous allez
avoir la solution à ce problème.
3 - Conclusion sur MiniMax
Il semblerait que les deux exemples abordés suffisent amplement
à montrer l'intérêt de minmax. Maintenant, vous devrez être capables de
créer votre propre procédure MinMax. Seule la fonction dévaluation vous
posera problème.
- Elaboration d'un arbre (Schéma) de conclusion
Pour conclure sur MinMax, nous allons proceder à création d'un
ultime arbre MinMax, dont nous allons aussi nous servir pour montrer les
problèmes de cet algorithme.

4 - Problèmes de MinMax
Evidemment Min-Max est bien pratique, mais arriver à des profondeurs
d'explorations d'arbres relativement grandes pose un énorme problème,
le temps d'attente. Par sa récursivité MinMax peut nous donner un arbre
de profondeur choisit, le temps de réponse varie de manière exponentielle.
Bien sûr, pour un jeu comme le morpion, ce temps est toujours très court
(environ 1 seconde pour tout l'arbre). Mais pour un jeu comme les échecs
ou l'Othello le temps peut devenir très long, déjà 1 minute d'attente
pour une profondeur de 8 coups et encore c'est très peu profond. Imaginez
que DeepBlue peut prévoir 50 coups d'échecs à l'avance, et qu'en une seconde
la solution est trouvée.
- A quels niveaux les optimisations sont-elles possibles
?
MinMax est donc optimisable sur l'exploration, cela veut dire
qu'il est possible de couper l'évaluation d'un partie de l'arbre, mais
sommes nous sûr de toujours gagner après avoir enlever certaines parties
de l'arbre... Sous le mystérieux nom d'Alpha-Beta se cache la solution.
[ La solution à toutes ces questions se trouve dans la partie de l'exposé Alpha-Beta. ]